Inverse design of three-dimensional surfaces via waterbomb tessellations

Abstract:

As a classical origami pattern, the waterbomb tessellation consisting of a set of waterbomb bases shows the potential to morph into three-dimensional surfaces by folding flat sheet materials. Here, we present an inverse-design method to approximate three-dimensional target surfaces based on this origami. First, we utilize the waterbomb base, in which six creases meet at the center, to generate a partially folded base mesh according to the target surface. Constraints of developability and flat-foldability are then solved through a gradient-based optimization on such a base mesh. In addition, we utilize the seven-crease waterbomb base, considered as a flat-foldable derivative of the six-crease waterbomb base, for approximating curved target surfaces. Another constraint of planarity is identified and solved, since the seven-crease waterbomb base contains two quads. Furthermore, we show the possibility of approximation via a combination of six- and seven-crease waterbomb bases. In optimization, Cartesian and parametric coordinates of vertices are adopted as unknown variables. We demonstrate the flexibility and validity of our method by illustrating a variety of origami approximations admitting geometric constraints. Our work not only facilitates the design of waterbomb tessellations as an art form, but also opens up avenues for future work on both theoretical structure analyses and novel engineering applications.

Unknown variables selection for optimizing waterbomb approximations

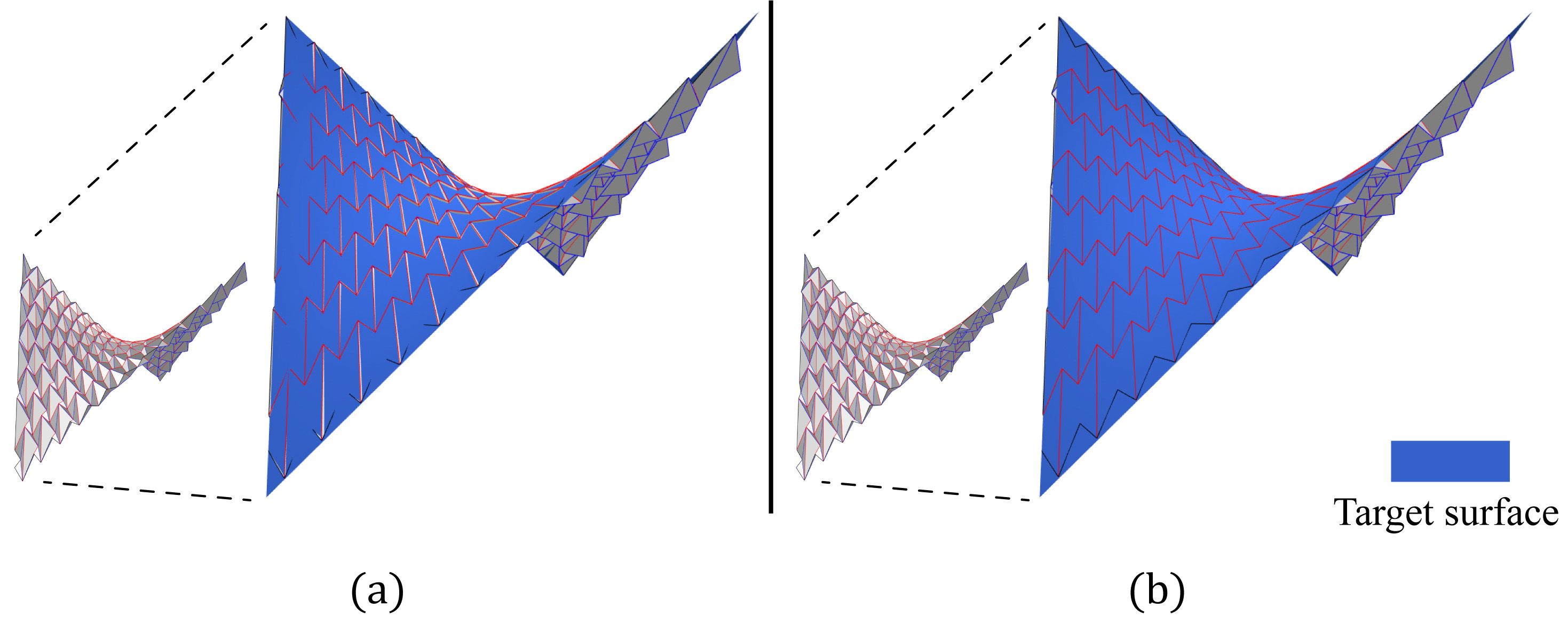
Resulting approximations of two target surfaces

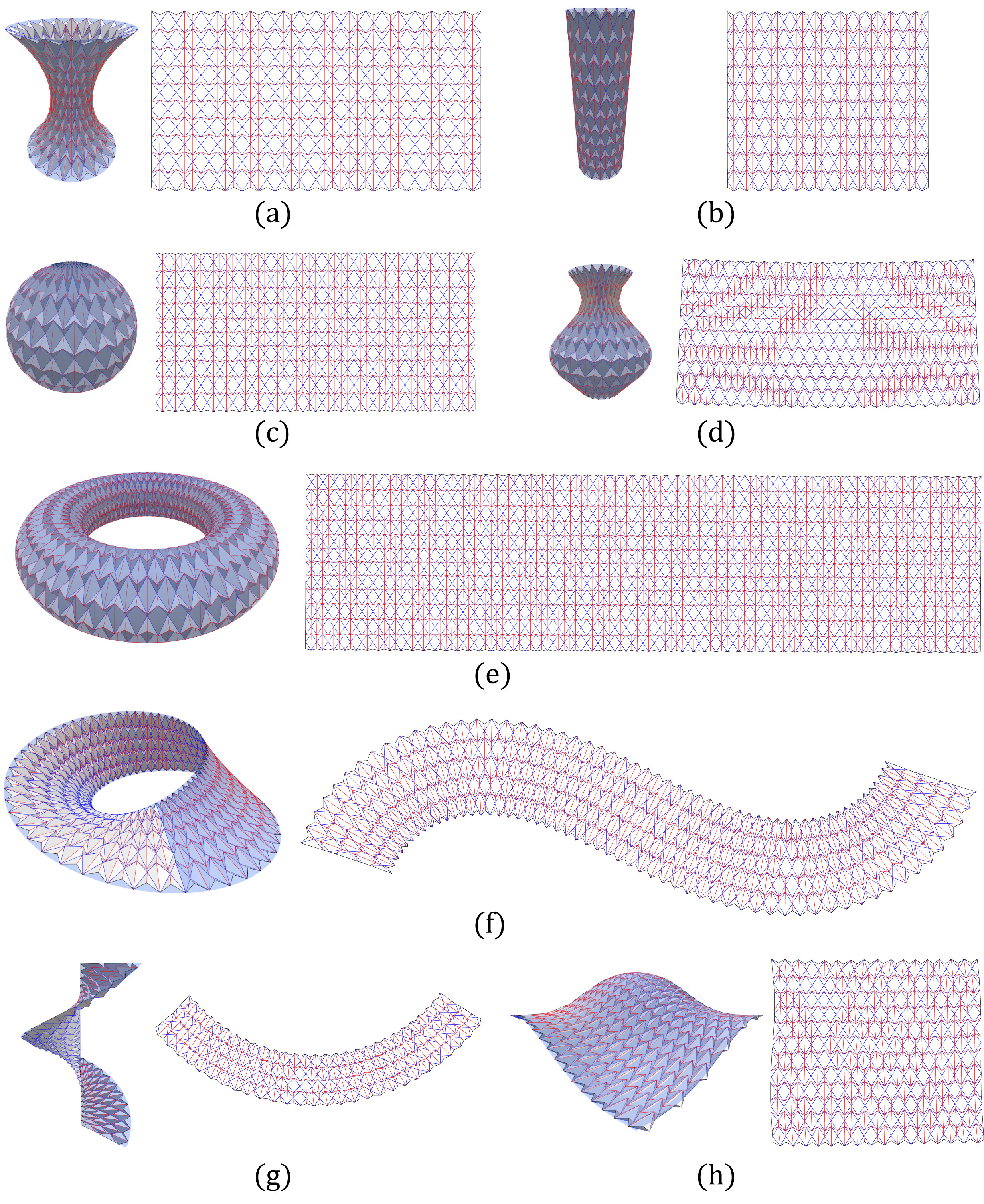
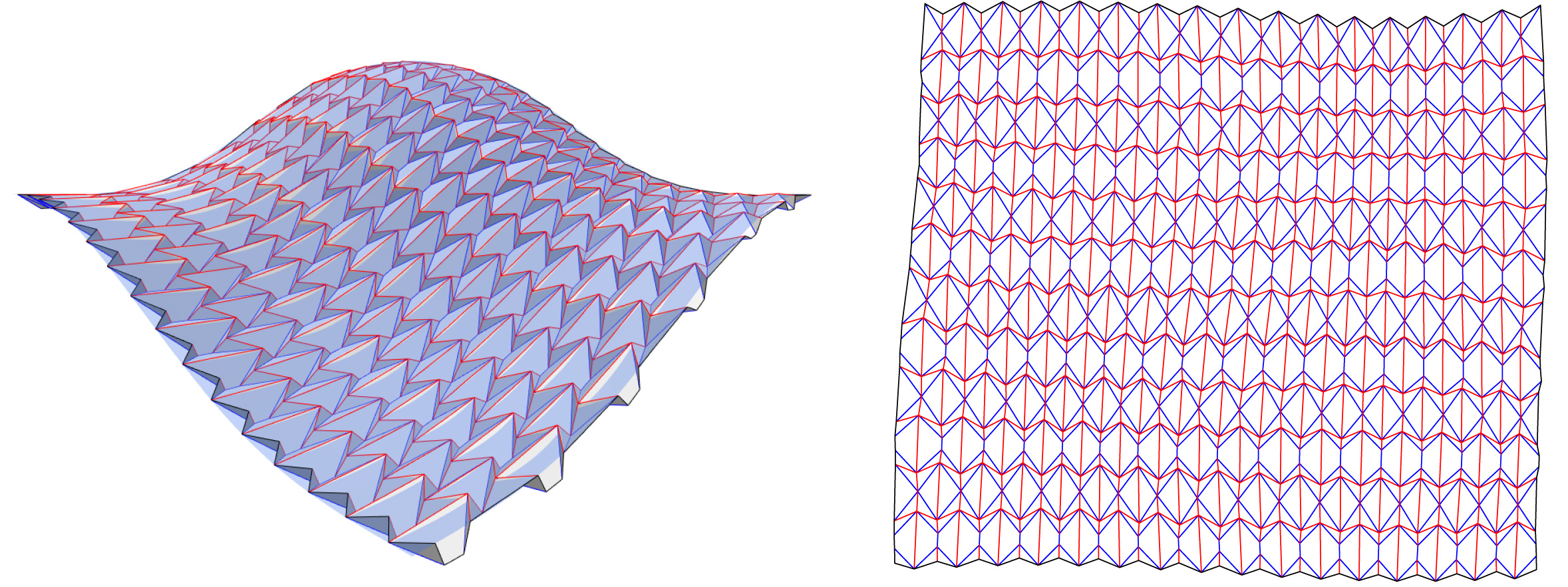
Resulting approximations via six-crease waterbomb bases

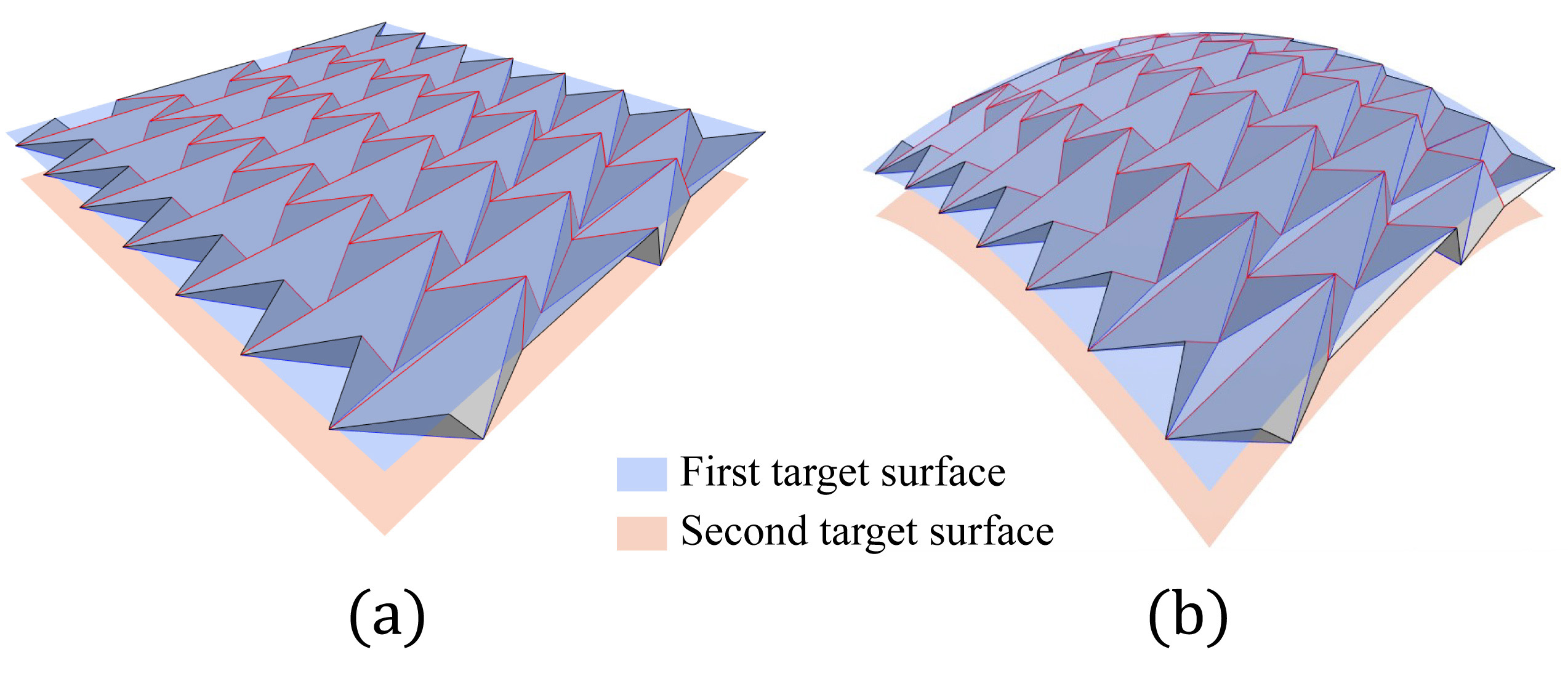
A resulting approximation with a combination of six- and seven-crease waterbomb bases