Computational Design Methods for Cylindrical and Axisymmetric Waterbomb Tessellations

Abstract:

Origami has provided a potential way to construct 3D curved structures by folding flat sheet materials without cutting or stretching. As a traditional origami, waterbomb tessellation is widely studied from aspects of science and engineering. However, users cannot easily utilize this kind of origami to fit curved target surfaces because the underlying geometric constraints limit the design space. In this study, we propose computational design methods for approximating cylindrical and axisymmetric curved surfaces based on waterbomb tessellations. With consideration of symmetry and periodic repetition, a single strip of the waterbomb tessellation is first modeled and then longitudinally and circumferentially replicated to construct cylindrical and axisymmetric waterbomb tessellations, respectively. To fulfill flat-foldability, an optimization process is introduced for minimizing flat-foldable residuals iteratively and then a regulation process of the crease pattern is applied for further reducing such residuals. In addition, we demonstrate waterbomb-derivative tessellations with quad-paddings to expand the design variations. Furthermore, rigid-folding sequences and several physically engineered origami pieces are presented. The proposed methods can be utilized to facilitate the design of origami-inspired structures for various engineering design purposes, such as foldable shelters, tubular structures, metamaterials, and so on.

Cylindrical approximations

Axisymmetric approximations

Waterbomb-derivative tessellations with quad-padding

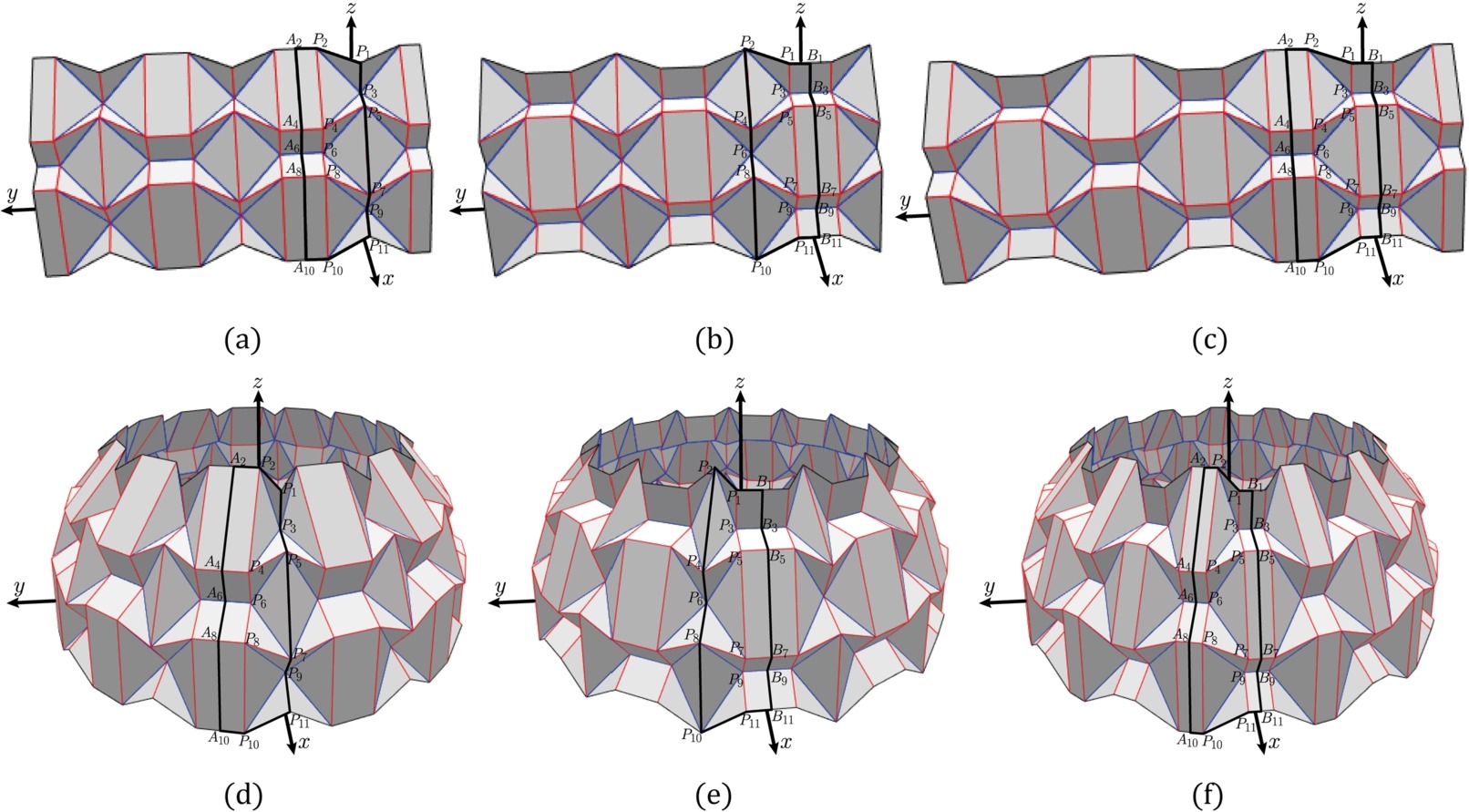
Animation of rigid-folding sequences for waterbomb tessellations.

Animation of rigid-folding sequences for waterbomb-derivative tessellations.